Refinements
Much of the discussion thus far has been based on rather ideal behaviors and/or system properties. Despite that, these analyses provide good “first-order” descriptions for the various components of the reed mechanism and together, capture the fundamental response of the overall system. Below, we discuss a number of incremental refinements that have been proposed to these equations.
- The motion of the reed is expected to induce a flow contribution of its own proportional to
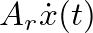 .
.
- The flow that enters the reed channel from the upstream side is therefore considered to divide into a component
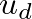 entering the downstream air column and the volume flow swept out by the reed,
entering the downstream air column and the volume flow swept out by the reed,
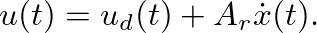 (37)
(37)
- This extra flow component has been shown to have some significant influence on playing frequencies as predicted from analytical and numerical simulations (Coyle et al., 2015).
- Stewart and Strong (1980) and Sommerfeldt and Strong (1988) modeled the reed as a damped, driven, nonuniform bar using a fourth-order differential equation. In this way, changes in effective mass and stiffness with bending along the curvature of the lay are automatically incorporated.
- Avanzini and van Walstijn (2004) also modeled the reed as a clamped-free bar using finite difference techniques and derived appropriate parameters from measurements and tuning. These results were then used to develop a non-linear lumped model (van Walstijn and Avanzini, 2007).
- More recent models of reed stiffness include an extra force term which only becomes active when the reed displacement goes beyond a certain distance, thus effectively producing a non-linear spring effect (Chatziioannou and van Walstijn, 2012).
- An additional force on the reed caused by higher localized volume flow within the reed channel was proposed by Worman (1971) and had been included in a few later reed analyses (Schumacher, 1981; Benade, 1976; Keefe, 1990b). For such a force to exist, the reed channel height must be non-uniform or the flow must separate at the channel entrance and then subsequently reattach at a further point in the channel. Hirschberg et al. (1990) point out that there are incompatibilities in the derivation of the “Bernoulli” force that make its application to the clarinet reed mechanism questionable.

| ©2004-2024 McGill University. All Rights Reserved.
Maintained by Gary P. Scavone.
|
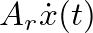 .
.
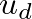 entering the downstream air column and the volume flow swept out by the reed,
entering the downstream air column and the volume flow swept out by the reed,
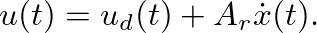 (37)
(37)
