Next: Register Hole Models Up: Tonehole Modeling Previous: A Two-Port Tonehole Model
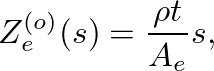 (11)
(11)
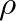 is the density of air,
is the density of air, 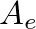 is the cross-sectional area of the end hole,
is the cross-sectional area of the end hole, 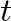 is the effective length of the opening (
is the effective length of the opening (
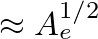 ), and
), and 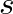 is the Laplace transform frequency variable.
is the Laplace transform frequency variable.
 is the characteristic impedance of the tonehole branch waveguide,
is the characteristic impedance of the tonehole branch waveguide, 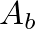 is the cross-sectional area of the branch and
is the cross-sectional area of the branch and 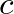 is the speed of sound.
is the speed of sound.
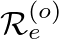 can be obtained using the conformal bilinear transform from the
can be obtained using the conformal bilinear transform from the 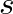 -plane to the
-plane to the 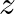 -plane (Oppenheim and Schafer, 1989, pp. 415-430), with the result
-plane (Oppenheim and Schafer, 1989, pp. 415-430), with the result
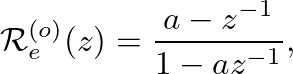 (13)
(13)
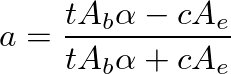 (14)
(14)
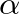 is the bilinear transform constant that controls frequency warping.
is the bilinear transform constant that controls frequency warping.
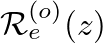 is a first-order allpass filter, which is consistent with reflection from a “masslike” impedance.
is a first-order allpass filter, which is consistent with reflection from a “masslike” impedance.
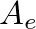 ) smoothly to zero.
) smoothly to zero.
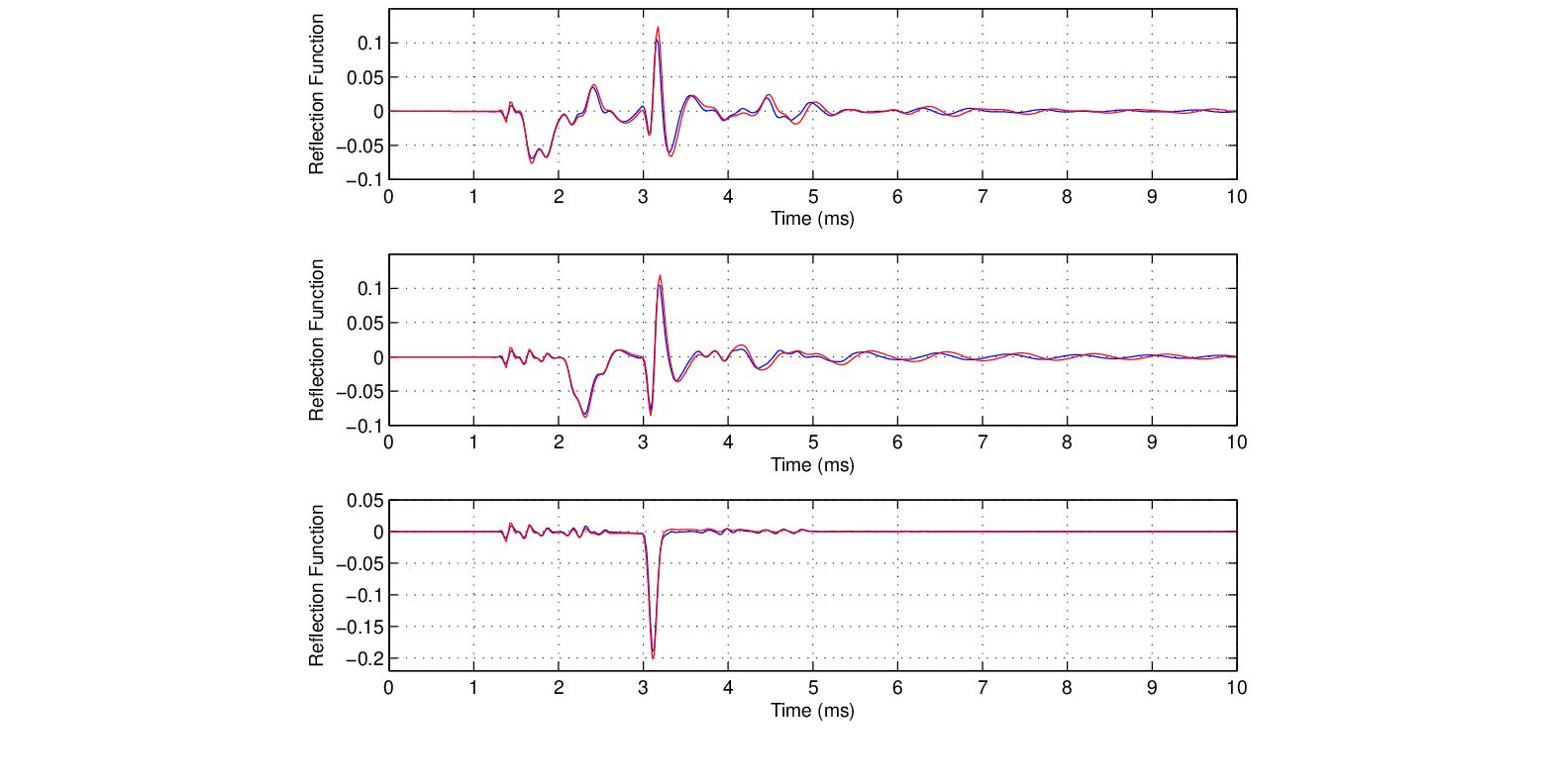
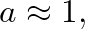 the reflectance phase delay is nearly zero for all frequencies, which corresponds well to pressure reflection at a rigid termination.
the reflectance phase delay is nearly zero for all frequencies, which corresponds well to pressure reflection at a rigid termination.
 |

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |