Next: Flow Through the Reed Orifice Up: Reed Valve Modeling Previous: Pressure-Controlled Reeds
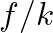 , where
, where 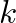 is the spring constant and
is the spring constant and 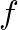 is the applied force.
is the applied force.
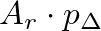 , where
, where 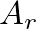 is the effective surface area of the reed exposed to
is the effective surface area of the reed exposed to 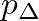 , the reed tip opening with respect to its equilibrium position
, the reed tip opening with respect to its equilibrium position 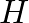 is given by Hooke's law as
is given by Hooke's law as
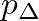 ) acting on it.
) acting on it.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |