Next: The Virtual “Blowed String” Up: Synthesizing Conical Instrument Sounds Previous: The “Cyclone”
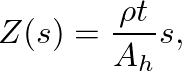
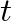 is the effective height of the hole and
is the effective height of the hole and 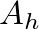 is its cross-sectional area.
is its cross-sectional area.
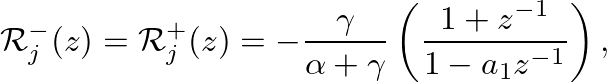
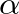 is the bilinear transform constant,
is the bilinear transform constant,
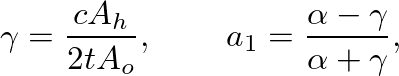
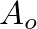 is the cross-sectional area of the cylindrical pipe.
is the cross-sectional area of the cylindrical pipe.
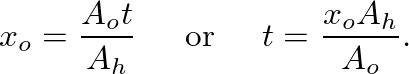
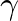 .
.
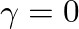 and
and
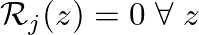 . Since there is no junction discontinuity, the system reduces to a single continuous cylindrical section.
. Since there is no junction discontinuity, the system reduces to a single continuous cylindrical section.
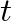 and
and 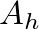 versus
versus 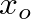 ), though its response is similar to the “cyclone” model.
), though its response is similar to the “cyclone” model.

| ©2004-2022 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |