Next: The Cylindrical Saxophone Up: Synthesizing Conical Instrument Sounds Previous: Modeling Approaches
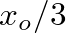 .
.
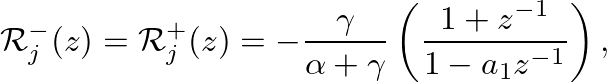
 is the bilinear transform constant,
is the bilinear transform constant,
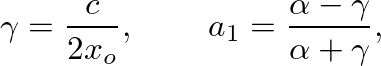
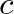 is the speed of wave propagation in the structure, and
is the speed of wave propagation in the structure, and 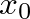 is the length of the truncated conic section.
is the length of the truncated conic section.
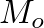 and the wave impedance of the input cylindrical section.
and the wave impedance of the input cylindrical section.
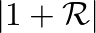 ) is shown in Fig. 20 for various values of
) is shown in Fig. 20 for various values of 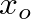 .
.
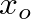 correspond to steeper flare rates, which produce greater wave discontinuity at the junction and greater low-frequency attenuation.
correspond to steeper flare rates, which produce greater wave discontinuity at the junction and greater low-frequency attenuation.
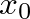 correspond to larger values of
correspond to larger values of 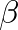 in Fig. 15 and thus greater mode inharmonicity. The result is a design conflict between junction discontinuity, which destabilizes the lower air column modes, and mode harmonicity.
in Fig. 15 and thus greater mode inharmonicity. The result is a design conflict between junction discontinuity, which destabilizes the lower air column modes, and mode harmonicity.

| ©2004-2022 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |