Next: Finite Length Cones Up: Conical Air Column Acoustics Previous: Conical Bores: Modes of Propagation
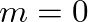 and
and 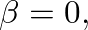 in which case Eq. (2) reduces to a general solution of the form
in which case Eq. (2) reduces to a general solution of the form
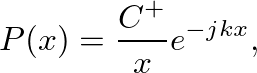 (3)
(3)
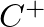 is a constant and
is a constant and 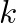 is the wave number in open air. Waves of this type will propagate at all frequencies.
is the wave number in open air. Waves of this type will propagate at all frequencies.
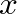 in a finite length conic section is composed of superposed spherical traveling-wave components of the form
where
in a finite length conic section is composed of superposed spherical traveling-wave components of the form
where 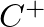 and
and 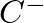 are complex amplitudes and sinusoidal time dependence is assumed.
are complex amplitudes and sinusoidal time dependence is assumed.
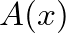 is the surface area of a spherical cap that intersects the principal axis of the pipe at position
is the surface area of a spherical cap that intersects the principal axis of the pipe at position 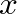 .
.
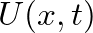 |
 |
![$\displaystyle \frac{A(x)}{x \rho c}\left[C^{+}\left(1 + \frac{1}{jkx}\right)e^{-jkx} -C^{-}\left(1 - \frac{1}{jkx}\right)e^{jkx}\right]e^{j\omega t},$](img42.png) |
|
 |
![$\displaystyle \frac{1}{x} \left[\frac{C^{+}}{Z_{c}(x)}e^{-jkx} - \frac{C^{-}}{Z_{c}^{*}(x)}e^{jkx}\right] e^{j\omega t}.$](img43.png) |
(6) |
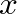 and frequency
and frequency 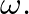
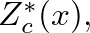 or the complex conjugate of
or the complex conjugate of 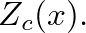
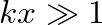 , the spherical wave fronts become more planar in shape and
, the spherical wave fronts become more planar in shape and 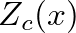 approaches
approaches 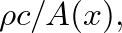 the wave impedance for plane waves in a duct of cross section
the wave impedance for plane waves in a duct of cross section 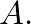
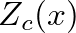 becomes increasingly dominant and in the limit as
becomes increasingly dominant and in the limit as
 the pressure and velocity traveling-wave components become
the pressure and velocity traveling-wave components become 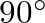 out of phase at the cone tip.
out of phase at the cone tip.
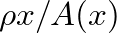 .
.

| ©2004-2022 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |