Next: Input Impedance Calculations Up: Conical Air Column Modeling Previous: Modeling a Single Conic Section
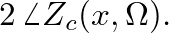
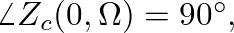 and pressure traveling-wave components reflect from the cone apex with a
and pressure traveling-wave components reflect from the cone apex with a  phase shift (or an inversion).
phase shift (or an inversion).
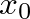 from its apex.
from its apex.
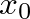 is found from the boundary condition
is found from the boundary condition 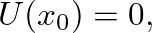 such that
such that
 is the Laplace transform variable and
is the Laplace transform variable and  is the speed of sound in air.
is the speed of sound in air.
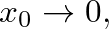 the reflectance approaches negative one as observed above.
the reflectance approaches negative one as observed above.
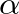 is the bilinear transform constant that controls frequency warping.
is the bilinear transform constant that controls frequency warping.
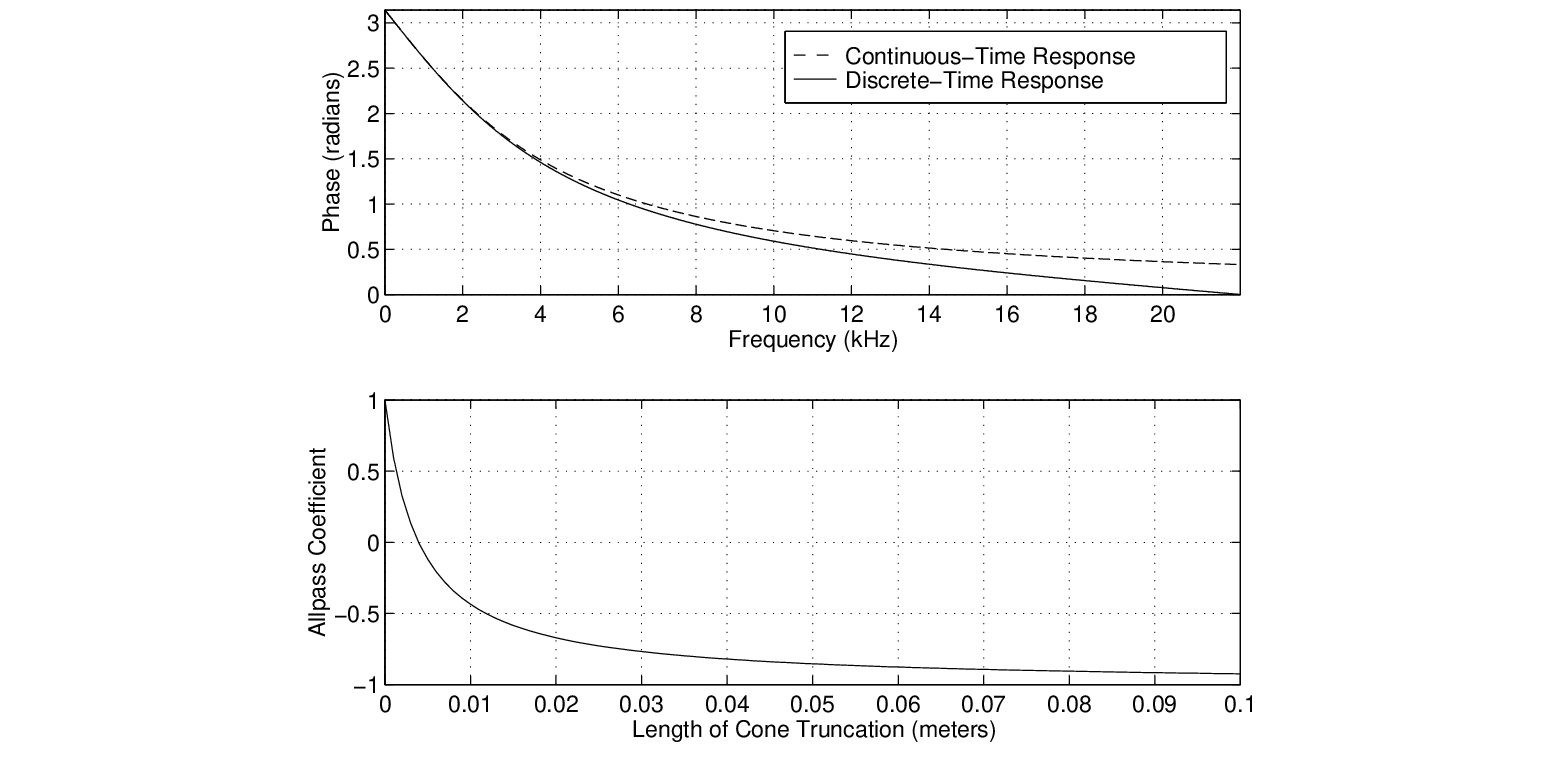
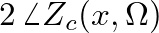 frequency-dependent phase delay experienced by pressure traveling-wave components reflecting from a rigid termination in a conical waveguide.
frequency-dependent phase delay experienced by pressure traveling-wave components reflecting from a rigid termination in a conical waveguide.
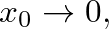 the filter becomes unstable because
the filter becomes unstable because
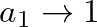 and the allpass pole falls on the unit circle. Thus, the truncation filter cannot be used to simulate a complete cone, but in this case the reflectance is simply negative one anyway.
and the allpass pole falls on the unit circle. Thus, the truncation filter cannot be used to simulate a complete cone, but in this case the reflectance is simply negative one anyway.
 |
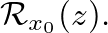

| ©2004-2022 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |