Lumped Elements:

1. The Ideal Dashpot:

   Figure 1: An ideal dashpot or damper.

   
   • The force necessary to overcome a mechanical dashpot or resistance is typically approximated as being proportional to velocity: $f(t) = \mu v(t) = \mu \frac{dx}{dt}$

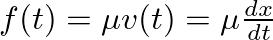
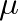   • The dashpot impedance is simply given by $\mu$, the frequency-independent damping constant.

   • The electrical correlate of a mechanical dashpot is a resistor, characterized by v(t) = R i(t). In an analog equivalent circuit, a dashpot can be represented by a resistor $R = \mu$.

2. The Ideal Mass:

   Figure 2: An ideal mass.

   
   • An ideal mass is assumed to move on a friction-less surface or guide-rod.

   • The ideal mass is completely rigid.

   • By Newton's Second Law: $f(t) = m a(t) = m \frac{dv}{dt} = m \frac{d^{2}x}{dt^{2}}$

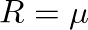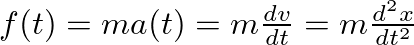
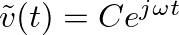   • If we assume the mass moves with a sinusoidal velocity $\tilde{v}(t) = C e^{j \omega t}$, where C is a complex constant, the corresponding force can be found by differentiation as: $\tilde{f}(t) = m j \omega \tilde{v}(t)$.

   • The frequency-domain mass impedance, assuming zero initial conditions, is then given by $Z_{m}(\omega) = F(\omega) / V(\omega) = m j \omega$.

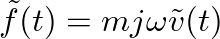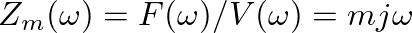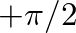   • The impedance of the mass corresponds to a frequency-dependent force response given a velocity input. At zero frequency it goes to zero (a constant DC velocity implies zero force) and it approaches infinity at high frequencies. The phase is $+\pi/2$: the force always leads velocity by a 1/4 cycle.

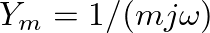   • The corresponding mass admittance (force input, velocity output) is $Y_{m} = 1/(m j \omega)$. A constant DC force produces an infinite velocity output, while a force of infinite frequency results in zero velocity (the mass resists high-frequency motion). The phase is 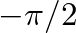$-\pi/2$: the velocity always lags the applied force by 1/4 cycle.

   • The electrical correlate of mechanical mass is an inductor, characterized by v(t) = L di/dt. In an analog equivalent circuit, a mass can be represented using an inductor with value L = m.

3. The Ideal Spring:

   Figure 3: An ideal spring.

   
   • The ideal spring has no mass or internal damping.

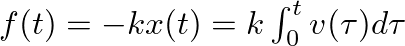   • By Hooke's Law: $f(t) = -k x(t) = k \int_{0}^{t} v(\tau) d\tau$ for x(0) = 0 (valid for small, non-distorting displacements)

   • The spring's equilibrium position is given by x=0.

   • A positive value of x produces a negative restoring force.

   • The spring constant k can also be referred to as the spring stiffness.

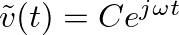   • If we assume the spring moves with a sinusoidal velocity $\tilde{v}(t) = C e^{j \omega t}$, where C is a complex constant, the corresponding force can be found by integration as: $\tilde{f}(t) = k \tilde{v}(t)/(j \omega)$.

   • The frequency-domain spring impedance, assuming zero initial conditions, is then given by $Z_{k}(\omega) = F(\omega) / V(\omega) = k / (j \omega)$.

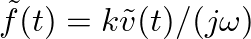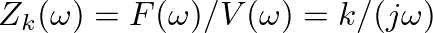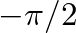   • The impedance of the spring (frequency-dependent velocity input, force output) at zero frequency approaches infinity (a constant DC velocity produces an infinite restoring force) and it goes to zero at high frequencies (the spring does not resist high-frequency motion). The phase is $-\pi/2$: the restoring force always lags velocity by a 1/4 cycle.

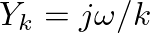   • The corresponding spring admittance (force input, velocity output) is $Y_{k} = j \omega / k$. A constant DC force implies a zero velocity output, while a force of infinite frequency results in an infinite velocity. The phase is 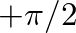$+\pi/2$: the velocity always leads the restoring force by 1/4 cycle.

   • The electrical correlate of a mechanical spring is a capacitor, characterized by i(t) = C dv/dt. In an analog equivalent circuit, a spring can be represented by a capacitor of value C = 1/k.

4. Mass / Spring Immittances using the Laplace Transform:
   • The Laplace transform is a convenient tool for analyzing continuous-time systems and solving differential equations, especially when taking into account initial conditions.

   • Applying the Laplace transform and the differentiation theorem to the ideal mass: F(s) = m[sV(s) - v(0)] = m[s²X(s) - sx₀ - v₀], where v₀ and x₀ are initial condition terms for velocity and displacement, respectively.

   • Assuming zero initial conditions, the mass impedance is given by Z_m(s) = F(s)/V(s) = m s and mass admittance is $Y_{m}(s) = V(s)/F(s) = \frac{1}{m s}$.

   • The inverse Laplace transform of the admittance,
     $$y_{m}(t) \ensuremath{\stackrel{\Delta}{=}}\mathcal{L}^{-1}\{Y_{m}(s)\} = \frac{1}{m} u(t),$$
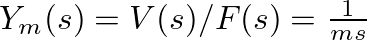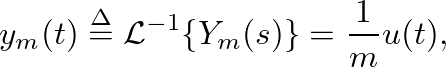
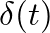     where u(t) is the unit step function, can be interpreted as the impulse response of the mass given an input $\delta(t)$ of velocity, which corresponds to transferring a unit of momentum to the mass at time 0, with a resulting velocity v(t) = 1/m.

   • Assuming zero initial conditions (x₀ = 0), the spring impedance is given by Z_k(s) = k / s and the spring admittance is Y_k(s) = s / k.