Free Vibrations of Ideal Systems:

In this section, we analyze the behaviour of particular combinations of masses, springs, and dashpots when given an initial displacement and/or velocity. We will consider forced oscillations in a subsequent section. The following linked online simulation provides useful visualizations for this section.

A Mass-Spring Oscillator

**Figure 4:** An ideal mass-spring system.
$\begin{figure}\begin{center} \epsfig{file=figures/mass-spring.eps, width=2.3in} \end{center} \end{figure}$

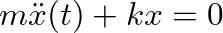
The series combination of an ideal mass and spring shown in Fig. 4 is characterized by the system equation: $m \ddot{x}(t) + k x = 0$
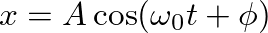This second-order homogeneous differential equation has solutions of the form $x = A \cos(\omega_{0}t + \phi)$ representing periodic motion.
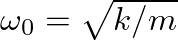$\omega_{0} = \sqrt{k/m}$ is the characteristic (or natural) angular frequency of the system.
A and $\phi$ are determined by the initial displacement and velocity.
There are no losses in the system, so it will oscillate forever.
This system can be analyzed using the Laplace transform with non-zero initial conditions as follows:
$\displaystyle m (s^2 X(s) - s x_{0} - v_{0}) + k X(s) = 0 \hspace{0.1in} \Longr... ... \frac{s x_{0}}{s^{2} + \omega_{o}^{2}} + \frac{v_{0}}{s^{2} + \omega_{o}^{2}}$
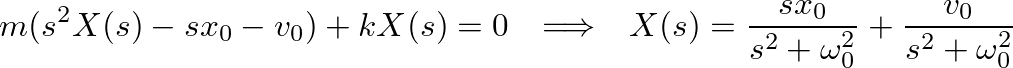
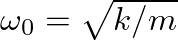where $\omega_{o} = \sqrt{k/m}$ . From a table of Laplace transform pairs, the solution is found as:
$\displaystyle x(t) = x_{0} \cos(\omega_{o} t) + \frac{v_{0}}{\omega_{o}} \sin(\omega_{o} t).$

A Damped Mass-Spring Oscillator

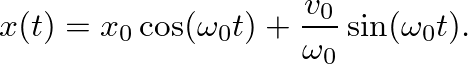
A physical system without losses is rare (if not impossible). The introduction of a mechanical dashpot in the mass-spring system provides damping and causes the resulting vibrations to decay over time.

**Figure 5:** An ideal mass-spring-damper system.
$\begin{figure}\begin{center} \epsfig{file=figures/msd.eps, width=3in} \end{center} \end{figure}$

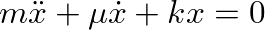
The series combination of an ideal mass, spring, and damper shown in Fig. 5 is characterized by the system equation: $m \ddot{x} + \mu \dot{x} + k x = 0$
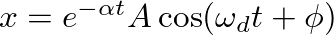This second-order homogeneous differential equation has solutions of the form $x = e^{-\alpha t} A \cos(\omega_{d}t + \phi)$ .

Figure 6: A decaying sinusoid.
$\begin{figure}\begin{center} \epsfig{file=figures/decaysin.eps, width=3.5in} \end{center} \end{figure}$
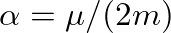$\alpha = \mu/(2m)$ is a decay constant and 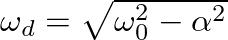$\omega_{d} = \sqrt{\omega_{0}^{2} - \alpha^{2}}$ is the characteristic (or natural) angular frequency of the system.
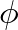A and $\phi$ are determined by the initial displacement and velocity.
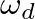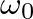The natural frequency $\omega_{d}$ is lower than that of the mass-spring system ( $\omega_{0}$ ).

**Figure 6:** A decaying sinusoid.
$\begin{figure}\begin{center} \epsfig{file=figures/decaysin.eps, width=3.5in} \end{center} \end{figure}$

A One-Mass, Two-Spring System

Longitudinal Motion (along x-axis):

Figure 7: A one-mass, two-spring system: Longitudinal motion.
$\begin{figure}\begin{center} \epsfig{file=figures/mass-twospring.eps, width=3in} \end{center} \end{figure}$
- The net restoring force on the mass: f_x(t) = -2 k x(t)
- System natural frequency: $\omega_{0} = \sqrt{2 k/m}$

**Figure 7:** A one-mass, two-spring system: Longitudinal motion.
$\begin{figure}\begin{center} \epsfig{file=figures/mass-twospring.eps, width=3in} \end{center} \end{figure}$

A Two-Mass, Three-Spring System

Longitudinal Motion (along x-axis):

Figure 8: A two-mass, three-spring system: Longitudinal motion.
$\begin{figure}\begin{center} \epsfig{file=figures/two-mass.eps, width=4in} \end{center} \end{figure}$
- System equations:
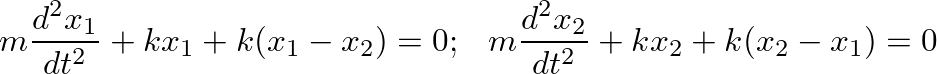
$\displaystyle m \frac{d^{2}x_{1}}{dt^{2}} + k x_{1} + k (x_{1} - x_{2}) = 0; \hspace{0.1in} m \frac{d^{2}x_{2}}{dt^{2}} + k x_{2} + k (x_{2} - x_{1}) = 0$
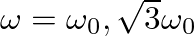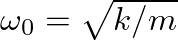
- Natural frequencies: $\omega = \omega_{0}, \sqrt{3}\omega_{0}$ , where $\omega_{0} = \sqrt{k/m}$

**Figure 8:** A two-mass, three-spring system: Longitudinal motion.
$\begin{figure}\begin{center} \epsfig{file=figures/two-mass.eps, width=4in} \end{center} \end{figure}$

Multiple Mass Systems

**Figure 9:** An infinite mass-spring system.
$\begin{figure}\begin{center} \epsfig{file=figures/mass-spring-etc.eps, width=6in} \end{center} \end{figure}$

Each additional mass-spring combination adds another natural mode of vibration per axis of motion.
As the number of masses and springs increases, the system begins to resemble a uniform string (assuming all masses and all springs are roughly equal in value). Eventually, it becomes more convenient to consider the mass and compression characteristics of the system to be uniformly distributed along its length (as we did in deriving the wave equation).