Next: References Up: Cylindrical Air Column Modeling Previous: Cylindrical Sections: Frequency-Domain Approach
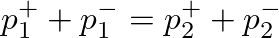 (46)
(46)
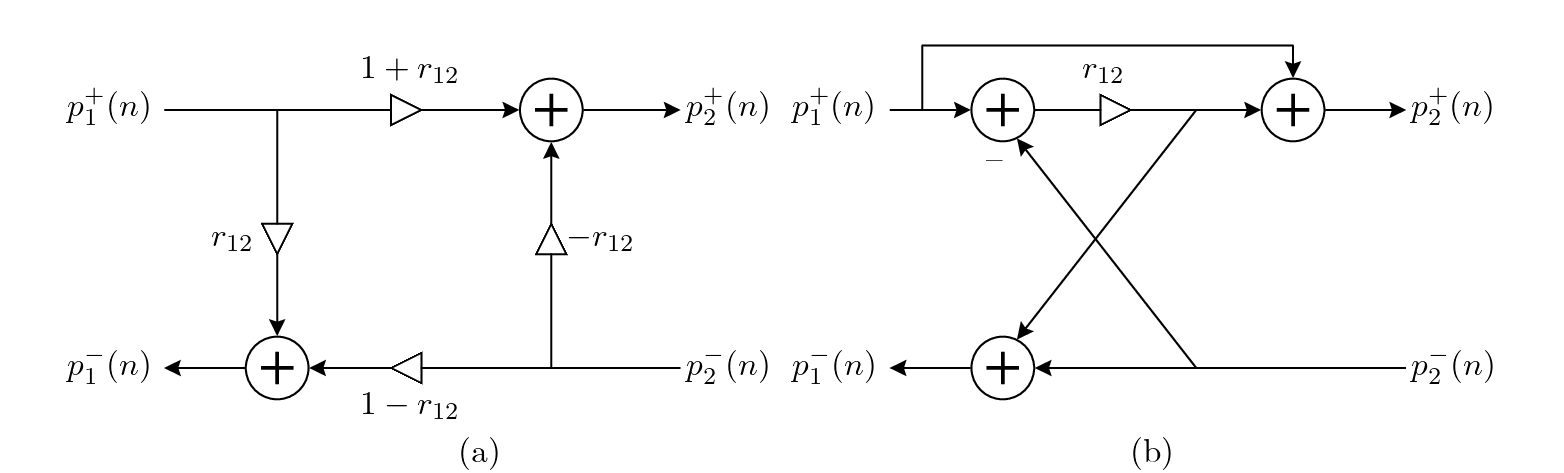
![$\displaystyle \frac{1}{Z_{c1}}\left[p_{1}^{+} - p_{1}^{-}\right] = \frac{1}{Z_{c2}}\left[p_{2}^{+} - p_{2}^{-}\right],
$](img172.png) (47)
(47)
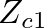 is the characteristic impedance of cylindrical section
is the characteristic impedance of cylindrical section  .
.
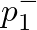 and
and 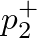 at the junction,
at the junction,
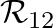 is the reflectance for the junction of cylinders
is the reflectance for the junction of cylinders 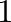 and
and 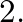
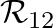 is given by
is given by
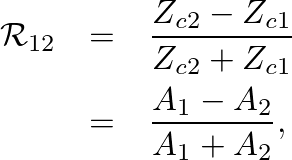
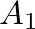 is the cross-sectional area of section
is the cross-sectional area of section 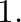
 |
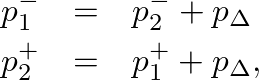
![$\displaystyle p_{\Delta} = \mathcal{R}_{12} \left[ p_{1}^{+} - p_{2}^{-} \right].
$](img190.png)

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |