Cylindrical Air Column Modeling

The acoustic behavior of wind-instrument air columns has traditionally been described in the frequency-domain, where such characteristics as normal-mode frequencies and decay rates and tonehole-lattice cutoff frequencies are easily identifiable. The requirements for wind-instrument bores are also typically stated in terms of frequency-domain constraints. Research on wind-instrument nonlinear excitation mechanisms and their complex coupling with the air column, as well as interest in the simulation of a complete wind instrument, however, has led to the development of time-domain models of wind-instrument sound production.

The linear time-domain response of an air column is represented by either its impulse response 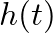$h(t)$ or its reflection function 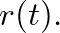$r(t).$ The impulse response is the pressure response at the bore entrance to the introduction of a unit volume velocity impulse. Because the entryway is represented by a closed end after the impulse is introduced, 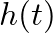$h(t)$ is a slowly decaying function. The reflection function is the pressure response at the entrance of the air column to the introduction of a unit pressure impulse. There are no reflections at the bore entryway for this response function, so that it decays to zero much more quickly than the impulse response. Traditional computational methods for the simulation of time-domain pressure propagation in a complete wind instrument involve the convolution of mouthpiece pressure with an air column response function during each time sample period. In this respect, 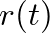$r(t)$ serves to greatly reduce the number of mathematical operations necessary for calculation of the model output. Digital waveguide modeling of wave propagation in wind-instrument air columns incorporates the advantages of the reflection function approach, and further reduces computational requirements by “pulling out” the delay inherent in 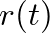$r(t)$ and implementing it in the form of digital delay lines.