Next: The Reed as a Mass-Spring-Damper Up: Reed Valve Modeling Previous: The Reed-Spring Solution
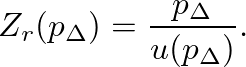 (25)
(25)
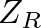 is given by:
is given by:
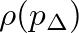 ) given by Eq. (27) and implemented via a scattering junction as shown in Fig. 13. The pressure entering the downstream instrument air column is determined as (Smith, 1986):
) given by Eq. (27) and implemented via a scattering junction as shown in Fig. 13. The pressure entering the downstream instrument air column is determined as (Smith, 1986):
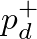 |
 |
![$\displaystyle p_{d}^{-} \cdot \rho(p_{\Delta}) + p_{u}^{+} \left[ 1 - \rho(p_{\Delta}) \right]$](img117.png) |
|
 |
![$\displaystyle p_{u}^{+} - \left[ p_{u}^{+} - p_{d}^{-} \right] \rho(p_{\Delta}).$](img118.png) |
(28) |
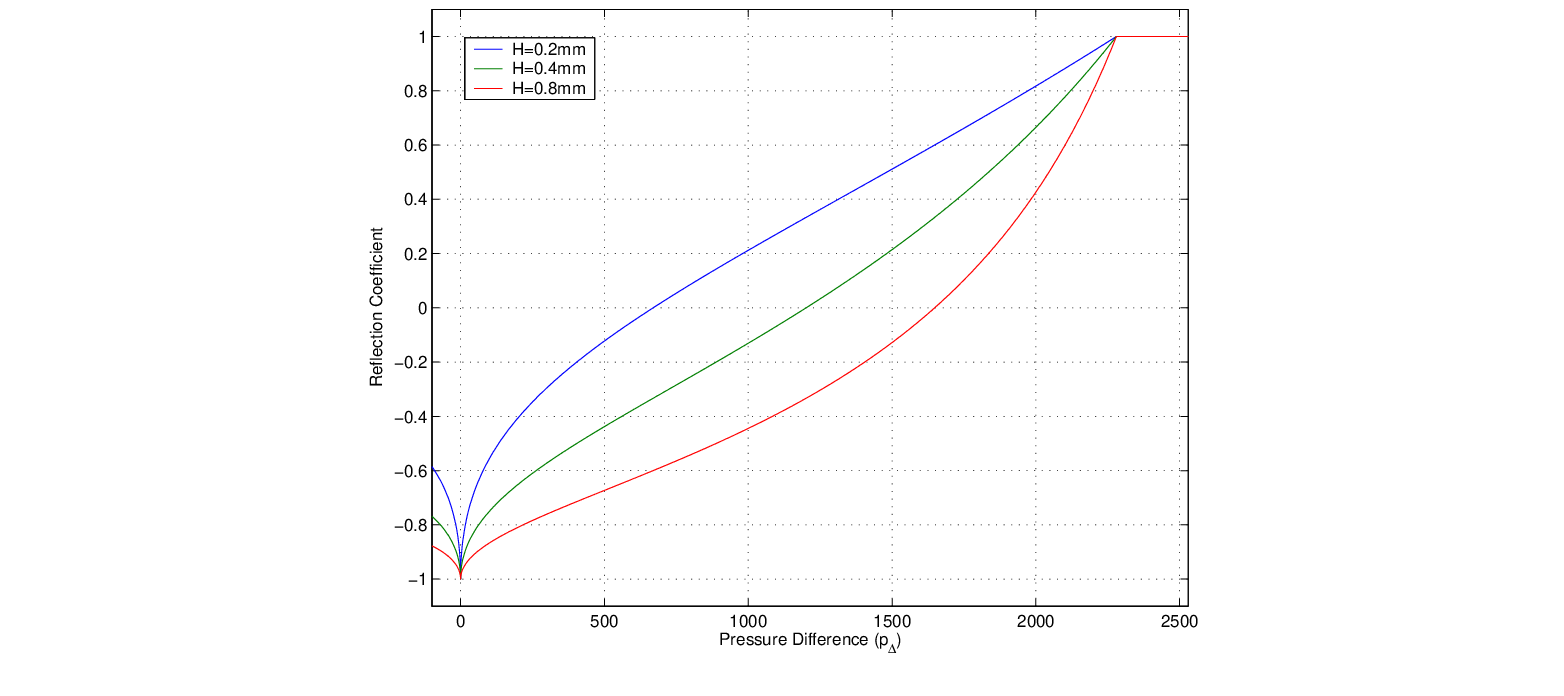 |
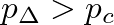 , the pressure reflection coefficient has unity gain. This corresponds to reflection from a rigidly stopped end, as mentioned previously.
, the pressure reflection coefficient has unity gain. This corresponds to reflection from a rigidly stopped end, as mentioned previously.
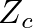 .
.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |