Next: The Mass-Spring-Damper Solution Up: Reed Valve Modeling Previous: Reed Scattering Theory
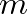 is the equivalent reed mass,
is the equivalent reed mass, 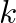 is the reed spring constant, and
is the reed spring constant, and 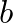 is the damping factor.
is the damping factor.
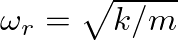 . Equation (29) is commonly expressed as
. Equation (29) is commonly expressed as
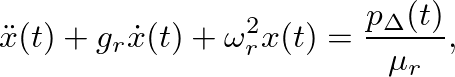 (30)
(30)
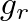 is the reed damping coefficient and
is the reed damping coefficient and 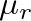 is the reed's dynamic mass per unit area.
is the reed's dynamic mass per unit area.

| ©2004-2024 McGill University. All Rights Reserved. Maintained by Gary P. Scavone. |